Sinus berekenen
Sinus berekenen
Ik vroeg mij af hoe oude rekenmachienes een Sinus konden bepalen.
Tegenwoordig plemp je gewoon een grote tabel in je machiene en dan ben je al een heel eind, maar vroeger was daar geen ruimte voor.
Welnu ik heb twee oplossingen bedacht die ik eens wilde proberen.
Manier 1)
Maak een tabel van 9 waarden, 0-8 overeen komend met de waarden 0 - 80 ' in stappen van 10 en vul daar de bijhorende Sinus waarde in.
Maak een tweede tabel van 10 waarden, 0-9 overeen komend 0 - 10' en vul daar ook de overeen komende waarden in.
Deze tabel is genoeg om zowel de Sinussen en Cosinussen van 0-360' in stapjes van 1' te bepalen.
Welnu: Sin(a+b) = Sin(a)Cos(b) + Sin(b)Cos(a)
Wil ik nu de sinus van 36' weten dan is dat dus Sin(30' + 6') = Sin(30)Cos(6)+Sin(6)Cos(30)
Manier 2)
Ik zorg dan ik de volgende twee waarden ken Sin(1') en Cos(1')
En daarmee kan ik wederom met de zelfde formule bij herhaling in stapjes van 1' blijven optellen.
Het apparaat rekent zich dan suf maar dan had ie maar geen rekenmachiene moeten worden
Moet lukken.
Echter al in mijn bed naar het plafon starend kwam ik er toch niet helemaal uit.
Ik nam in gedachten de bekende 3-4-5 driehoek, met bekende hoeken van 30, 60 en 90 graden.
Daar geld dus Sin(30)=3/5, Cos(30)=4/5 Sin(60)=4/5 en Cos(60)=3/5
Als ik nu de sinus van twee hoeken van 30' wil weten doe ik dus het volgende
Sin(30 + 30) = Sin(30)*Cos(30) + Sin(30)*Cos(30) = (3/5 * 4/5) + (4/5 * 3/5) = (12/25 + 12/25) = 24/25
Terwijl ik natuurlijk als antwoord Sin(60) = 4/5 verwacht.
Goed... waar ga ik de mist in ?
Tegenwoordig plemp je gewoon een grote tabel in je machiene en dan ben je al een heel eind, maar vroeger was daar geen ruimte voor.
Welnu ik heb twee oplossingen bedacht die ik eens wilde proberen.
Manier 1)
Maak een tabel van 9 waarden, 0-8 overeen komend met de waarden 0 - 80 ' in stappen van 10 en vul daar de bijhorende Sinus waarde in.
Maak een tweede tabel van 10 waarden, 0-9 overeen komend 0 - 10' en vul daar ook de overeen komende waarden in.
Deze tabel is genoeg om zowel de Sinussen en Cosinussen van 0-360' in stapjes van 1' te bepalen.
Welnu: Sin(a+b) = Sin(a)Cos(b) + Sin(b)Cos(a)
Wil ik nu de sinus van 36' weten dan is dat dus Sin(30' + 6') = Sin(30)Cos(6)+Sin(6)Cos(30)
Manier 2)
Ik zorg dan ik de volgende twee waarden ken Sin(1') en Cos(1')
En daarmee kan ik wederom met de zelfde formule bij herhaling in stapjes van 1' blijven optellen.
Het apparaat rekent zich dan suf maar dan had ie maar geen rekenmachiene moeten worden
Moet lukken.
Echter al in mijn bed naar het plafon starend kwam ik er toch niet helemaal uit.
Ik nam in gedachten de bekende 3-4-5 driehoek, met bekende hoeken van 30, 60 en 90 graden.
Daar geld dus Sin(30)=3/5, Cos(30)=4/5 Sin(60)=4/5 en Cos(60)=3/5
Als ik nu de sinus van twee hoeken van 30' wil weten doe ik dus het volgende
Sin(30 + 30) = Sin(30)*Cos(30) + Sin(30)*Cos(30) = (3/5 * 4/5) + (4/5 * 3/5) = (12/25 + 12/25) = 24/25
Terwijl ik natuurlijk als antwoord Sin(60) = 4/5 verwacht.
Goed... waar ga ik de mist in ?
Vivo ergo onus
- vi coactus
- Berichten: 228
- Lid geworden op: zo jan 19, 2020 12:02 pm
Re: Sinus berekenen
Zie wikipedia, genoeg manieren om de sinus te bepalen of te benaderen.
Voor kleine waardes geldt overigens sin(x)=x
Verder hoef je maar één van de twee te kennen, vanuit de sinus kun je de cosinus bepalen en vv.
Voor kleine waardes geldt overigens sin(x)=x
Verder hoef je maar één van de twee te kennen, vanuit de sinus kun je de cosinus bepalen en vv.
Re: Sinus berekenen
Bij mijn weten geld dat idd voor tan bij heeel kleine waarden.robert schreef: Zie wikipedia, genoeg manieren om de sinus te bepalen of te benaderen.
Voor kleine waardes geldt overigens sin(x)=x
Van sin ben ik daar niet zeker van.
Je zult de ander moeten bepalen om de berekening voort te zetten.robert schreef: Verder hoef je maar één van de twee te kennen, vanuit de sinus kun je de cosinus bepalen en vv.
Vivo ergo onus
Re: Sinus berekenen
Hoe oud? Volgens mij wordt CORDIC al behoorlijk lang gebruikt en heeft geen bijster grote tabellen nodig.pascal schreef: wo mei 20, 2020 10:24 pm Ik vroeg mij af hoe oude rekenmachienes een Sinus konden bepalen.
Maar waarom ik eigenlijk wou reageren is dit brilljante artikel:
http://www.righto.com/2020/05/extractin ... -math.html
Re: Sinus berekenen
Verdikke Daniel, je hebt gelijk, Cordic heb ik zelf al eens in vhdl geinplementeerd (al heb ik geen idee meer hoe)
ja zo'n 8087 CoProfessor moet ik ook nog ergens hebben liggen,
Lui die dat soort dingen doen (zijn er niet veel maar wel een paar) zijn wel echte freaks hoor.
Dank je voor de leuke link
ja zo'n 8087 CoProfessor moet ik ook nog ergens hebben liggen,
Lui die dat soort dingen doen (zijn er niet veel maar wel een paar) zijn wel echte freaks hoor.
Dank je voor de leuke link
Vivo ergo onus
Re: Sinus berekenen
Ik was nieuwsgierig hoe nauwkeurig de 'taylor-approximatie' is
https://en.wikipedia.org/wiki/Sine#Series_definition
met een polynoom van de 7e graad (is dat Nederlands)? Niet dat dit de beste methode is en je kunt het vast wiskundig bewijzen, maar ook leuk om empirisch te doen. Hier de code:
https://gist.github.com/danieldk/a4a661 ... 520bb6064e
Uitkomst:
Ik zou er niet meteen een raket mee naar de maan schieten, maar leuk hoe je met zo'n simpele benadering zo dichtbij kan komen.
https://en.wikipedia.org/wiki/Sine#Series_definition
met een polynoom van de 7e graad (is dat Nederlands)? Niet dat dit de beste methode is en je kunt het vast wiskundig bewijzen, maar ook leuk om empirisch te doen. Hier de code:
https://gist.github.com/danieldk/a4a661 ... 520bb6064e
Uitkomst:
Code: Selecteer alles
$ python sin.py
Avg/min/max delta: 7.63e-03/0.00e+00/7.52e-02
- vi coactus
- Berichten: 228
- Lid geworden op: zo jan 19, 2020 12:02 pm
Re: Sinus berekenen
Dat is Nederlands ja. Taylor series zijn leuk ja, opzich.iswrong schreef: wo mei 27, 2020 8:45 pm Ik was nieuwsgierig hoe nauwkeurig de 'taylor-approximatie' is
https://en.wikipedia.org/wiki/Sine#Series_definition
met een polynoom van de 7e graad (is dat Nederlands)? Niet dat dit de beste methode is en je kunt het vast wiskundig bewijzen, maar ook leuk om empirisch te doen. Hier de code:
https://gist.github.com/danieldk/a4a661 ... 520bb6064e
Uitkomst:
Ik zou er niet meteen een raket mee naar de maan schieten, maar leuk hoe je met zo'n simpele benadering zo dichtbij kan komen.Code: Selecteer alles
$ python sin.py Avg/min/max delta: 7.63e-03/0.00e+00/7.52e-02
Maar ik heb veel met power, Fourier en Taylor (en welke dan ook nog meer) series moeten doen wat het al minder leuk maakt. Sowieso kijken of ze convergeren. Maar ook recurrente betrekkingen maken voor de coefficienten, die moet je dan vaak weer delen in even en oneven (a_(2k), a_(2k+1)).
Maar het is een super manier om dingen te vereenvoudigen zonder de nauwkeurigheid kwijt te raken die je wenst. Met een 2e of 3e orde (orde en graads worden alletwee gebruikt vziw) ben je er al snel.
Het is sowieso leuker en beter om met letters te rekenen in het algemeen. Ik gebruikte nooit bv 296794533 m/s als input voor de snelheid van een deeltje, maar 0.99c.
Reden is ook simpel.. In alle formules gebruik je v/c,en dan bijvoorbeeld /(1-v/c) of /(1-(v/c)^2).. 0.99c/c=0.99
Bij het Nederlands MeetInstituut heb ik veel geleerd over en gebruik gemaakt van onnauwkeurigheidanalyse en significante cijfers. Lang niet altijd heb je tig cijfers nodig. Je moet alleen wel even weten hoeveel en wanneer en veel mensen maken dus ook fouten met 1 getallen opschrijven en 2 het de juiste afronding.
Overigens ben ik fan van software zoals maple, die kan aardig overweg met rekenen met letters. En kun je dus even snel iets proberen of je afleiding controleren. Volgens mij bestaat er niet een oss programma voor, voor matlab heb je octave die best goed werkt.
Re: Sinus berekenen
Nog even machine code (Intel-stijl, x86_64), gecompileerd vanaf Rust:
Min of meer zoals je het zou verwachten. Belangrijkste verandering die de compiler maakt is aftrekken te vervangen door sommeren en de constanten waar nodig te vervangen door -constante.
Code: Selecteer alles
.LCPI0_0:
.long 3233808384
.LCPI0_1:
.long 1123024896
.LCPI0_2:
.long 3315433472
example::poor_mans_sine:
movaps xmm1, xmm0
mulss xmm1, xmm0
movaps xmm2, xmm0
mulss xmm2, xmm1
mulss xmm1, xmm1
movaps xmm3, xmm2
divss xmm3, dword ptr [rip + .LCPI0_0]
addss xmm3, xmm0
mulss xmm0, xmm1
divss xmm0, dword ptr [rip + .LCPI0_1]
addss xmm0, xmm3
mulss xmm1, xmm2
divss xmm1, dword ptr [rip + .LCPI0_2]
addss xmm1, xmm0
movaps xmm0, xmm1
ret
Re: Sinus berekenen
Dank je Daniel,
Ik moet weer even in intel assembly code (dat heb ik nu echt al 30 jaar niet meer gedaan daar ik vooral met embedded CPU;s werk)
maar mooie van je voorbeeld is dat ik dat prima naar vhdl kan porten.
Ik moet weer even in intel assembly code (dat heb ik nu echt al 30 jaar niet meer gedaan daar ik vooral met embedded CPU;s werk)
maar mooie van je voorbeeld is dat ik dat prima naar vhdl kan porten.
Vivo ergo onus
Re: Sinus berekenen
Ik kwam er niet zo snel uit, intel is niet echt de CPU waarop ik assembly placht te doen.
Dus maar even uitgezocht wat het idee van Jack Volder ook weer was.
Dit heb ik even geprobeerd in een stukje javascript en dat blijkt verassend snel tot een goed resultaat te leiden
Hier een snippet van mijn implementatie
Dus maar even uitgezocht wat het idee van Jack Volder ook weer was.
Dit heb ik even geprobeerd in een stukje javascript en dat blijkt verassend snel tot een goed resultaat te leiden
Hier een snippet van mijn implementatie
Code: Selecteer alles
Max_X = 512;
Max_Y = 384;
Half_Y = Max_Y/2; // halve hoogte waar de 'virtulele' nul ligt
Half_X = Max_X/2; // 180' oftwewel Pi
Quart_X = Half_X/2; // 90' om zodoende met de sin functie een cos te kunnen bepalen
this.SineAprox = function(x)
{
var X = x - Math.round(x/Max_X);
var s;
if(x<Half_X)
s = (x - 0) * (x - Half_X) / 16500;
else
s = - (x - Half_X) * (x - Max_X) / 16500;
return s;
}
Vivo ergo onus
Re: Sinus berekenen
Vandaag een VHDL implementatie gemaakt die op basis van bovenstaande op een FPGA een sinewave genereert.
Ik moet het nog even uitwerken, dan zal ik het hier posten.
Ik moet het nog even uitwerken, dan zal ik het hier posten.
Vivo ergo onus
Re: Sinus berekenen
Pfff gewoon niet de tijd om alles met foto's ed online te zetten, eens kijken hoever ik nu kom
Hier een linkje voor de hele code
Dit zijn de resultaten

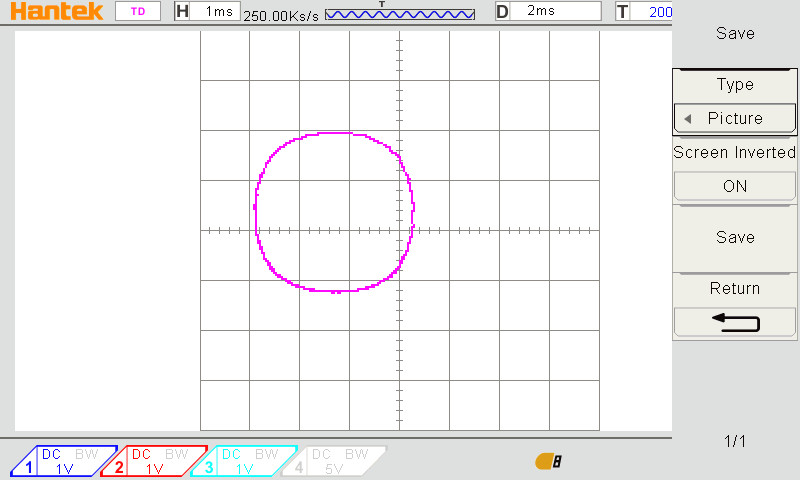
Een allerzinds bevredigend resultaat

Hier zie je dat het toch echt om een benadering gaat en de circel niet precies rond is.
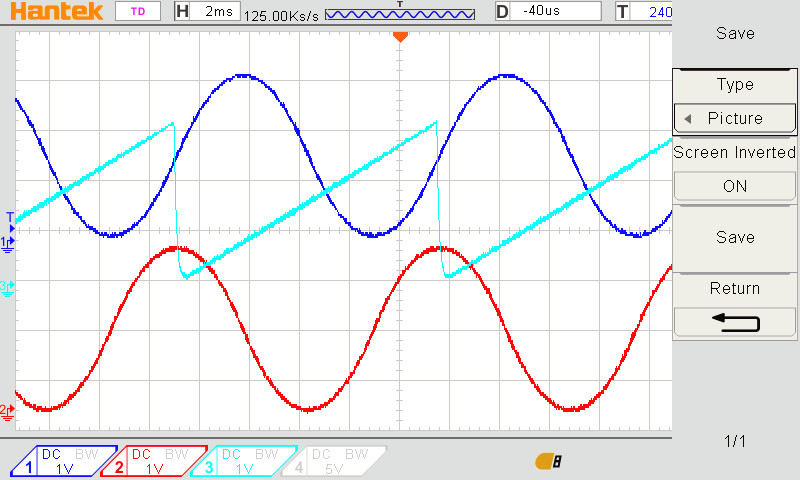
Mijn analoge 4ch scope is helaas stuk, toch wilde ik laten zien dat de software DAC prima werkt, zie de lineariteit van de zaagtand
Om het geheel dan toch maar compleet te maken
Hier een linkje voor de hele code
Code: Selecteer alles
-- Title : Cordic
-- Function : Cordic Implementation
-- Author : Pascal Schiks (C) 2020 GNU/GPL, Meaning anyone can copy use and modify this code for selfeducation and leasure.
-- Board : RZ_EasyFPGA
-- FPGA : EP4CE6E22C8
-- ConfigDev : EPS4N BS03X
-- Notes
-- The purpose of this experiment is to generate a Sine/Cosine wave using an aproximation algorithm
-- such not using an sinewave table.
-- The 3 PwmOut pins are to be connected to a RC LowPass Filter, where R=2k2 and C=47nF,
-- Asci art impression of this: FPGApin ---===---+---||-----Gnd
-- 2k2 47nF
-- Where the scope should be hooked op at the + sign
-- Scope settings for all channels 1V/Div, timebase 2ms/Dev (the output is aprox 90Hz)
-- Chan 1 and 2 show Sine and Cosine, while Chan 3 optional is to show the linearity (or more nonelinearity) of the DAC
-- Also Sync is not realy required as the scope realy tiggers well on the signal
-- Setting the scope in X/Y mode should show a perfect circle which it doesn't, after all it's an aproximation.
library ieee;
use ieee.std_logic_1164.all;
use ieee.std_logic_unsigned.all;
use ieee.std_logic_arith.all;
use ieee.numeric_std.all;
entity Cordic is
port
(
PwmOut : Out std_logic_vector(3 DownTo 1) := "000";
SyncOut : Out std_logic := '0';
CLK50MHz : IN std_logic
);
End entity Cordic;
Architecture cordic_demo of Cordic is
-- ClockSignals
signal ClkDiv : std_logic_vector(31 downto 0);
signal WaveClk : std_logic;
signal PwmClk : std_logic;
-- PWM Signals
signal PwmCnt : Integer Range 0 to 300 := 0;
type PwmType is array(1 to 3) of Integer Range 0 To 255;
signal PwmVal : PwmType := (others=>0);
-- CORDIC signals
signal Alpha : Integer Range 0 to 520 := 0;
constant TwoPi : Integer := 512;
constant Pi : Integer := 256;
constant HalfPi : Integer := 128;
constant Gain : Integer := 129;
constant Offset : Integer := 128;
-- Pin assignment straight into the source
attribute chip_pin: string;
attribute chip_pin of PwmOut : signal is "86,98,84";
attribute chip_pin of syncOut : signal is "103";
attribute chip_pin of Clk50MHz : signal is "23";
-- Aproximation of Sinewave
Function Sine(X : Integer Range 0 to 1024) return Integer Is
Variable Xmod2Pi : Integer Range 0 to 512;
Begin
XMod2Pi := X Mod TwoPi;
If Xmod2Pi > Pi Then
return (((Xmod2Pi - Pi) * (Xmod2Pi - TwoPi)) / Gain) - Offset;
Else
return Offset - (((Xmod2Pi - 0) * (Xmod2Pi - Pi)) / Gain);
End If;
End Function Sine;
--
-- Main program
--
Begin
-- Generate reqiured clock signals
ClockDivider : Process (Clk50MHz)
Begin
if Clk50MHz'Event and Clk50MHz='1' then
ClkDiv <= ClkDiv + '1';
end if;
PwmClk <= ClkDiv(0);
WaveClk <= ClkDiv(9);
end process;
-- Single pin PWM based DAC Then requires only a simple RC LowPassFilter
PwmGenerator : Process (PwmClk)
Begin
If PwmClk'Event and PwmClk='1' Then
-- Counter
If PwmCnt < 255 Then
PwmCnt <= PwmCnt+1;
Else
PwmCnt <= 0;
End If;
-- PWM-DAC 1- 3
For ch in 1 to 3 loop
If PwmVal(ch) > PwmCnt Then
PwmOut(ch) <= '1';
Else
PwmOut(ch) <= '0';
End If;
End Loop;
End If;
End Process PwmGenerator;
-- The SineWave aproximation
CordicWaveGenerator : Process (WaveClk)
Begin
If WaveClk'Event And waveClk='1' Then
-- Phase progression ranging from 0 to 2*Pi
If Alpha < TwoPi Then
Alpha <= Alpha + 1;
Else
Alpha <= 0;
End If;
-- Sync
If Alpha < HalfPi Then
SyncOut <= '1';
Else
SyncOut <= '0';
End If;
PwmVal(1) <= Sine(Alpha);
PwmVal(2) <= Sine(Alpha+HalfPi);
PwmVal(3) <= Alpha / 2;
End If;
End Process CordicWaveGenerator;
End cordic_demo;

Een allerzinds bevredigend resultaat

Hier zie je dat het toch echt om een benadering gaat en de circel niet precies rond is.

Mijn analoge 4ch scope is helaas stuk, toch wilde ik laten zien dat de software DAC prima werkt, zie de lineariteit van de zaagtand

Om het geheel dan toch maar compleet te maken
Vivo ergo onus
Re: Sinus berekenen
Ik vind wiskunde wel boeiend alleen is mijn wiskundekennis vrij beperkt.
Re: Sinus berekenen
Overigens heb ik wel onlangs het boek van Matt Parker (die ik heb leren kennen via zijn YouTube-video's over wiskunde) The Humble Pi) gekocht en met veel plezier gelezen. Er is een nederlandse vertaling maar de reviews bij Bol.com zijn daar uiterst kritisch over dus ik heb maar de engelse versie genomen
Re: Sinus berekenen
Ha Jovo, ik heb ook geen math held hoor. Heb ik een maatje voor die helemaal in zn element zit als ik zoiets vraag.
Maar even naar de code kijkend kun je ziet dat het idd een Sinus benadering genereerd en dat het ook een prima oplossing is.
Echter geen cordic
Mischien iets voor komende week, dan heb ik een paar dagen vrij.
Maar even naar de code kijkend kun je ziet dat het idd een Sinus benadering genereerd en dat het ook een prima oplossing is.
Echter geen cordic
Mischien iets voor komende week, dan heb ik een paar dagen vrij.
Vivo ergo onus